Modelo de simulación de Monte Cario - Part 6

Modelo de simulación de Monte Cario - Part 5

Modelo de simulación de Monte Cario - Part 4

Modelo de simulación de Monte Cario - Part 3

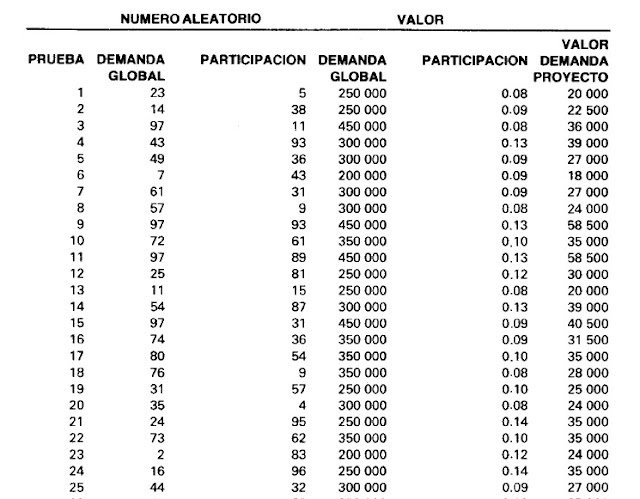
La asignación de números representativos se efectúa en proporción a la pro- babilidad acumulada. Así, por ejemplo, si el 10% se encuentra en el rango de hasta 200 000, deben asignarse 10 números representativos (0 al 9). Como hasta 250 000 hay un 35% de probabilidades, se asignan 35 números representativos (0 al 34).

La etapa siguiente del modelo requiere tomar al azar números aleatorios. Para ello, se puede usar una tabla de números aleatorios como la de la Figura 18.2. Cada número seleccionado debe ubicarse en la columna "Asignación de números repre- sentativos". Una vez localizado, se da el valor correspondiente de demanda global, el cual se ajusta por el porcentaje de participación en el mercado obtenido de igual forma. Por ejemplo, si se usa la tabla de números aleatorios de arriba hacia absyo, se encuentra que el primer número es 23, el cual se ubica en el rango 10-34 de la asignación de números representativos, del cuadro de demanda global, lo que hace seleccionar el primer valor de 250 000. El segundo número aleatorio es 05, el cual se ubica en el rango 0-25 de la asignación de números representativos de la participación del proyecto en el mercado, lo que hace seleccionar el valor de 0.08. De acuerdo con esto, la demanda esperada para el proyecto en el primer año corresponde a: 

Dp = 250 000 x 0.08 = 20 000 

En el mismo procedimiento se repite un número suficiente de veces como para que la probabilidad de elegir entre todos los resultados posibles, guarde estrecha relación con sus distribuciones de probabilidades. En el ejemplo, se toman 100 pruebas para cada variable, obteniéndose los resultados que se indican.

Modelo de simulación de Monte Cario - Part 2

Supóngase, además, que la demanda global del mercado está correlacionada con la tasa de crecimiento de la población, que se estima en un 2% anual a futuro. El precio y los costos asociados al proyecto se suponen conocidos o menos incierto su resultado futuro. El primer paso en la solución consiste en expresar matemáticamente el pro- blema. En este caso, la demanda por año que podría enfrentar el proyecto se puede expresar como: 

Dp = Dg.p 

donde Dp corresponde a la demanda del proyecto, Dg a la demanda global y p al porcentaje de participación del proyecto en el mercado. La tasa de crecimiento de la demanda se incorporará al final como un factor de incremento sobre la demanda del proyecto. Una forma alternativa es incorpo- rarlo en la fórmula anterior, lo que permite obtener el mismo resultado pero con cálculos más complejos. El siguiente paso del método Monte Cario es la especificación de la distribución de probabilidades de cada variable. En el ejemplo, las variables que deben especi- ficar su distribución de probabilidades son la demanda global del mercado y la participación del proyecto. En ambos casos se deberá posteriormente calcular la distribución de probabilidad acumulada y la asignación de rangos de números entre 0 y 99 (o sea, 100 números). A continuación se muestran estos cálculos para las dos variables en estudio.

Modelo de simulación de Monte Cario - Part 1

El modelo de Monte Cario, llamado también método de ensayos estadísticos, es una técnica de simulación de situaciones inciertas que permite definir valores esperados para variables no controlables, mediante la selección aleatoria de valores, donde la probabilidad de elegir entre todos los resultados posibles está en estricta relación con sus respectivas distribuciones de probabilidades. Si las variables inciertas relevantes en un proyecto fuesen, por ejemplo, la demanda y la participación de mercado, deberá aplicarse en ambas la simulación para estimar su comportamiento en el futuro. Supóngase que estudios realizados señalan que la demanda global esperada del mercado tiene la siguiente distribución de probabilidades:

Uso del árbol de decisión - III

Por lo tanto, la decisión será ampliar a nivel nacional, porque retorna un VAN esperado mayor. La siguiente decisión se refiere a la introducción inicial. Si es a nivel regional, existe un 70% de posibilidades de que la demanda sea alta. Si así fuese, el VAN esperado sería de 1 900, que correspondería al resultado de la decisión que se tomaría de encontrarse en ese punto de decisión. Aplicando el procedimiento anterior, se obtiene:

Uso del árbol de decisión - II

Por ejemplo, la última decisión de nuestro caso es la [2], que presenta dos sucesos de alternativa. El valor esperado del suceso (C) se calcula aplicando la fórmula 18.2, de la siguiente forma:

Uso del árbol de decisión - I

El árbol de decisión es una técnica gráfica que permite representar y analizar una serie de decisiones futuras de carácter secuencial a través del tiempo. Cada decisión se representa gráficamente por un cuadrado con un número dispuesto en una bifurcación del árbol de decisión. Cada rama que se origina en este punto representa una alternativa de acción. Además de los puntos de decisión, en este árbol se expresan, mediante círculos, los sucesos aleatorios que influyen en los resultados. A cada rama que parte de estos sucesos se le asigna una pro- babilidad de ocurrencia. De esta forma, el árbol representa todas las com- binaciones posiblesxle decisiones y sucesos, permitiendo estimar un valor esperado del resultado final, como un valor actual neto, utilidad u otro. Supóngase, a manera de ejemplo, que se estudia el lanzamiento de ún nuevo producto. Las posibilidades en estudio son introducirlo en nivel nacional o regional. Si se decide lanzar el producto regionalmente, es posible posteriormente hacerlo a nivel nacional, si el resultado regional así lo recomendara. En la Figura 18.1 se representa un diagrama de un árbol de decisión para este caso, en el cual cada ramificación conduce a un cierto valor actual neto diferente.

Para tomar la decisión óptima, se analizan los sucesos de las alternativas de desición más cercanas ai final del árbol, calculando el valor esperado de sus valores actuales netos y optando por aquélla que proporcione el mayor valor esperado del VAN.

El método de la equivalencia a certidumbre - V

Un procedimiento distinto sugiere John Cañada9 para tratar la equivalencia por certeza, o método de expectativa y variaciones, como él lo denomina, consis- tente en determinar la variación de la expectativa relacionando el resultado previsto con la variación de ese resultado, mediante la expresión:

El método de la equivalencia a certidumbre - IV

Si ambas tasas permanecen constantes y si f es mayor que i, puede demostrarse que at es mayor que a,+1. O sea, al permanecer constante la tasa de descuento ¿gustada por riesgo, los coeficientes de conversión a condiciones de equivalente por certeza serían decrecientes y el riesgo crecería en el tiempo. De esta forma, el método de la tasa de descuento ajustada por riesgo supone que el riesgo aumenta por el tiempo per se. No puede afirmarse que existe riesgo por tiempo, pero sí que el riesgo puede ser mayor si los condicionantes del proyecto en el tiempo tienen un riesgo mayor. Van Horne8 ejemplifica el caso de una plantación forestal cuyo riesgo, más que aumentar, decrecería en el tiempo. De esto Van Horne con- cluye que "la presunción de un riesgo creciente no sería apropiada para este caso, y el proyecto de plantación sería penalizado si utilizáramos el método de tasa de descuento ajustada por riesgo. 

Con el método de conversión a condiciones equiva- lentes por certeza, la gerencia puede especificar directamente el grado de riesgo para cada período futuro en particular, y luego descontar el flujo de caja empleando la tasa que representa el valor tiempo del dinero". Esta posición parece ser bastante razonable, puesto que permite ayustar el riesgo a cada período y no al proyecto en su coryunto, como sería al emplear la tasa de descuento. De esta forma, es posible considerar que el riesgo puede variar en el tiempo en función de que los factores condicionantes del proyecto en el tiempo tengan un riesgo con carácter variable.

El método de la equivalencia a certidumbre - III

Robichek y Myers7 hacen un interesante análisis para demostrar que este método es superior ai del ajuste a la tasa de descuento. Para ello suponen que la tasa de descuento ^justada por riesgo (0 y la tasa libre de riesgo (i) permanecen constantes. Si ambos métodos fueran correctos, el resultado de un ajuste a la tasa de descuento debería ser igual al ajuste a condiciones del equivalente a certeza. Para un período t cualquiera, se tendría:

El método de la equivalencia a certidumbre - II

Al expresar todos los' flujos de caja en su equivalencia de certeza, puede evaluarse el proyecto a través del VAN, actualizando estos flujos a la tasa libre de riesgo (i), mediante la siguiente expresión:

El índice t del coeficiente a indica que éste puede variar en un mismo proyecto a través del tiempo. La aplicación de este método permite descontar los flujos sólo considerando el factor tiempo del uso del dinero, sin incorporar en la tasa de descuento el efecto 

El índice t del coeficiente a indica que éste puede variar en un mismo proyecto a través del tiempo. La aplicación de este método permite descontar los flujos sólo considerando el factor tiempo del uso del dinero, sin incorporar en la tasa de descuento el efecto del riesgo. Sin embargo, en la práctica resulta muy difícil la conversión al equiva- lente de certeza de los flujos de caja.

El método de la equivalencia a certidumbre - I

La equivalencia a certidumbre es un procedimiento de alternativa al método de la tasa de descuento ajustada por riesgo. Según este método, el flujo de caja del proyecto debe ayustarse por un factor que represente un punto de indiferencia entre un fliyo del que se tenga certeza y el valor esperado de un flujo sujeto a riesgo. Si se define este factor como a, se tiene que:

donde at es el factor de ajuste que se aplicará a los flujos de caja inciertos en el período t; BNC, representa el flujo de caja en el período t sobre el que se tiene certeza y BNRt representa el flujo de caja incierto en el período t. El factor del coeficiente a varía en forma inversamente proporcional al grado de riesgo. A mayor riesgo asociado, menor será el coeficiente a, cuyo valor estará entre cero y uno. Weston y Brigham6 explican el concepto de equivalencia de certeza ejemplifi- cando una situación en que debe optarse por una de dos alternativas: a) recibir $ 1 000 000 si al tirar al aire una moneda perfecta resulta cara, sin obtener nada si sale sello y b) no tirar la moneda y recibir $ 300 000. El valor esperado de la primera opción es $ 500 000 (0.5 x 1 000 000 + 0.5 x 0). Si el jugador se muestra indiferente entre las dos alternativas, los $ 300 000 son el equivalente de certeza de un rendimiento esperado de $ 500 000 con riesgo. Al reemplazar mediante estos valores en la expresión 18.11, se tiene:

 

El método del ajuste a la tasa de descuento - II

Para ajustar adecuadamente la tasa de descuento, se define una curva de indiferencia del mercado cuya función relaciona el riesgo y los rendimientos con la tasa de descuento. La curva de indiferencia del mercado se ilustra en el Gráfico 18.1, cuyos ejes representan la tasa de rendimiento necesaria y el riesgo expresado en términos de un coeficiente de variación. La curva de indiferencia del mercado graficada indica que los flujos de caja asociados a un evento sin riesgo se descuentan a una tasa libre de riesgo del 5%, que corresponde a una situación de certeza. Los puntos B, C y D indican qué para coeficientes de variación de 0.6, 1.0 y 1.4 se precisan tasas de descuento de 8.10 y 12%, respectivamente. Al aumentar el riesgo de un proyecto se necesitan rendi- mientos mayores para que ameriten aprobarse. De esta forma, el mayor grado de riesgo se compensa por una mayor tasa de descuento que tiende a castigar el proyecto. De acuerdo con esto, el cálculo del valor actual neto se efectúa mediante la siguiente fórmula: La dificultad de este método reside en la determinación de la prima por riesgo. Al tener un carácter subjetivo, las preferencias personales harán diferir la tasa adicional por riesgo entre distintos inversionistas para un mismo proyecto.

El método del ajuste a la tasa de descuento - I

Una forma de ajustar ios flujos de c^ja consiste en hacerlo mediante correcciones en la tasa de descuento. A mayor riesgo, mayor debe ser la tasa para castigar la rentabilidad del proyecto. De esta forma; un proyecto rentable evaluado en función de una tasa libre de riesgo puede resultar no rentable, si se descuenta a una tasa ^justada. El principal problema de este método es determinar la tasa de descuento apropiada para cada proyecto. Al no considerar explícitamente información tan relevante como la distribución de probabilidades del fliyo de c^ja proyectado, muchos autores definen este método como una aproximación imperfecta para incorporar el factor riesgo a los proyectos.

Dependencia e independencia de los flujos de caja en el tiempo - V

La dificultad práctica más relevante es la necesidad de clasificar como independientes o perfectamente correlacionadas a las distintas variables del fliyo de c^ja. David Hertz6 propuso un modelo de simulación integral para calcular los resultados probables, así como su dispersión. Su modelo se basa en la definición de 9 factores principales del proyecto que influyen en el resultado de la evaluación: dimensión del mercado, precios de venta, tasa de crecimiento del mercado, parti- cipación en el mercado, inversión requerida, valor de recuperación de la inversión, costos operativos, costos fijos y vida útil de los equipos. Para cada factor se estiman los valores probables que asumiría y se le asigna una probabilidad de ocurrencia a cada valor sólo como referencia. Sin calcular un valor esperado de cada factor se combinan al azar los 9 factores para valores probables cambiantes. Es decir, se calculan distintos rendimientos sobre la inver- sión simulando valores cambiantes para cada uno de los 9 factores. 

Con los resultados observados mediante este procedimiento se elabora una tabla de frecuencia sobre la que se calcula el resultado probable y su dispersión o riesgo. El modelo de simulación de Hertz es similar a uno de los criterios de análisis de sensibilidad que se desarrolla en el próximo capítulo. Sin embargo, el modelo se ampliará generalizándolo al uso de cualquier variable y para calcular no sólo la tasa media de rendimiento sobre la inversión, sino que cualquiera de los criterios de decisión analizados en el capítulo anterior.

Dependencia e independencia de los flujos de caja en el tiempo - IV

La desviación estándar de los flujos de caja perfectamente correlacionados de un proyecto se calcula aplicando la siguiente expresión: Esto confirma que cuando los fliyos de caja están perfectamente correlaciona- dos, la desviación estándar y el riesgo son mayores que cuando existe independencia entre ellos. Cuando los flujos de csya no se encuentran perfectamente correlacionados, es posible aplicar el modelo de correlación intermedia desarrollado por Frederick Hillier. En él se plantea que la desviación estándar para un flujo de caja que no está perfectamente correlacionado se encuentra en algún punto intermedio entre las dos desviaciones antes calculadas. El problema de su cálculo reside en que incorpora en un mismo modelo tanto flujos perfectamente correlacionados como independientes. 

Dependencia e independencia de los flujos de caja en el tiempo - III

Aplicando la expresión 18.2, se obtiene que los valores esperados de ios flujos de caja para cada período son $ 50 000, $ 40 000 y $ 30 000. De acuerdo con la fórmula 18.4, el valor esperado del VAN es, para una tasa libre de riesgo del 6%, de $ 7 958. Recurriendo a una tabla de distribución normal, se obtiene que la probabilidad que se deseaba averiguar corresponde aproximadamente al 33%. Hasta ahora se ha supuesto que los filaos de caga son independientes entre sí a lo largo del tiempo. Sin embargo, en la mayoría de los proyectos existe cierta dependencia entre los resultados de dos períodos. Es importante saber si existe o no dependencia entre los fliyos, por las consecuencias que tienen sobre el análisis del riesgo. Si los filaos son dependientes, o sea, si están correlacionados a través del tiempo, la desviación estándar de la distribución de probabilidad de los valores actuales netos probables es mayor que si fueran independientes. A mayor correla- ción, mayor dispersión de la distribución de probabilidad. Los fliyos de c^ja estarán perfectamente correlacionados si la desviación del fliyo de caja de un período alrededor de la media de la distribución de probabilidades en ese período implica que en todos los períodos futuros el fliyo de csya se desviará exactamente de igual manera.

Dependencia e independencia de los flujos de caja en el tiempo - II

Además de la información proporcionada por las expresiones 18.4 y 18.6, es posible calcular la probabilidad de que el VAN sea superior o inferior a cierto monto de referencia. Para ello se resta el valor esperado del valor actual neto calculado en la expresión 18.4 de ese valor de referencia y se divide su resultado por la desviación estándar. Esto es:

donde z es la variable estandarizada o el número de desviaciones estándar de la inedia (valor esperado del VAN). Para determinar la probabilidad de que el VAN del proyecto sea menor o igual que x, se acude a una tabla de distribución normal, que muestra el área de la distribución normal que es x desviaciones estándares hacia la izquierda o derecha de la media. 

Para ilustrar la aplicación de estas fórmulas, supóngase la existencia de una propuesta de inversión que requiere en el momento cero de $ 100 000. Los filaos de cíya futuros se proyectan a tres períodos con las siguientes probabilidades de ocurrencia:

 

Aplicando la expresión 18.2, se obtiene que los valores esperados de los flujos de c

Dependencia e independencia de los flujos de caja en el tiempo - I

El análisis de riesgo en los proyectos de inversión se realiza de distinta forma según los filaos de caja en el tiempo, sean o no dependientes entre sí. Es decir, si el resultado de un período depende o no de lo que haya pasado en otro período anterior. Cuando hay independencia entre las distribuciones de probabilidad de los fliyos de csya futuros, el valor esperado del valor actual neto sería 

 

donde i es la tasa de descuento libre de riesgo. La desviación estándar de la distribución de probabilidades de este valor actual neto es:

que corresponde a la desviación estándar alrededor del valor esperado calculado por la expresión 18.4.

Métodos para tratar el riesgo

Para incluir el efecto del factor riesgo en la evaluación de proyectos de inversión se han desarrollado diversos métodos o enfoques que no siempre conducen a un idéntico resultado. La información disponible es, una vez más, uno de los elementos determinantes en la elección de uno u otro método. El criterio subjetivo es uno de los métodos más comúnmente utilizados. 

Se basa en consideraciones de carácter informal de quien toma la decisión, no incorporando específicamente el riesgo del proyecto, salvo en su apreciación personal. Se ha intentado mejorar este método sugiriendo que se considere la expectativa media y la desviación estándar del VAN, lo cual, aunque otorga un carácter más objetivo a la inclusión del riesgo, no logra incorporarlo en toda su magnitud. 

De igual forma, el análisis de fluctuaciones de los valores optimistas, más probables y pesimistas del rendimiento del proyecto, sólo disminuye el grado de subjetividad de la evaluación del riesgo, pero sin eliminarla. Los métodos basados en mediciones estadísticas son quizás los' que logran superar en mejor forma, aunque no definitivamente, el riesgo asociado a cada proyecto. Para ello, analizan la distribución de probabilidades de los flujos futuros de cuya para presentar a quien tome la decisión de aprobación o rechazo los valores probables de los rendimientos y de la dispersión de su distribución de probabilidad. En el apartado 18.4 se analiza este método para los casos de dependencia e independencia del flujo de caja respecto del tiempo.

Un método diferente de inclusión del riesgo en la evaluación es el del ajuste a la tasa de descuento. Con este método, el análisis se efectúa sólo sobre la tasa pertinente de descuento, sin entrar a ajustar o evaluar los flujos de-caja del proyecto. Si bien este método presenta serias deficiencias, en términos prácticos es un procedimiento que permite solucionar las principales dificultades del riesgo. En la sección 18.5 se aborda nuevamente este tema. Frente a las desventajas (que posteriormente se analizarán) respecto al método de ajuste a la tasa de descuento y con similares beneficios de orden práctico, está el método de la equivalencia a certidumbre. Según este criterio, quien decide está en condiciones de determinar su punto de indiferencia entre flujos de caja por percibir con certeza y otros, obviamente mayores, sujetos a riesgo. La sección 18.6. se destina a analizar este método. Otro de los criterios que es preciso evaluar es el de los valores esperados. Este método, conocido comúnmente como análisis del árbol de decisiones, combina las probabilidades de ocurrencia de los resultados parciales y finales para calcular el valor esperado de su rendimiento. Aunque no incluye directamente la variabilidad de los flujos de caja del proyecto, ajusta los fliyos al riesgo en función de la asignación de probabilidades. El apartado 18.7 se ocupa de este procedimiento. El último método que se estudia en este texto es el análisis de sensibilidad, que si bien es una forma especial de considerar el riesgo, se analiza como caso particular en el capítulo 19, por la importancia práctica que ha adquirido. La aplicación de este criterio permite definir el efecto que téndrían sobre el resultado de la evaluación cambios en uno o más de los valores estimados en sus parámetros.

La medición del riesgo - III

Si hubiera otra alternativa de inversión cuya desviación estándar fuese mayor que $ 387.30, su riesgo sería mayor, puesto que estaría indicando una mayor dispersión de sus resultados. La desviación estándar, como se verá luego, se utiliza para determinar la probabilidad de ocurrencia de un hecho. No es adecuado utilizarla como única medida de riesgo, porque no 'discrimina en función del valor esperado. De esta forma, dos alternativas con valores esperados diferentes de sus retornos netos de fondos pueden tener desviaciones estándares iguales, requiriendo de una medición complementaria para identificar diferenciaciones en el riesgo. El coeficiente de variación es, en este sentido, una unidad de medida de la dispersión relativa, que se calcula por la expresión 

 

Aun cuando dos alternativas pudieran presentar desviaciones estándares iguales, si los valores esperados de sus flujos de caja son diferentes, este procedimiento indicará que mientras mayor sea el coeficiente de variación, mayor es el riesgo relativo

La medición del riesgo - II

Para ejemplificar la determinación del valor esperado y de la desviación estándar, supóngase la existencia de un proyecto que presente la siguiente distribución de probabilidades de sus flujos de caja estimados:

La medición del riesgo - I

Se definió el riesgo de un proyecto como la variabilidad de los flujos de caja reales respecto a los estimados. Ahora corresponde analizar las formas de medición de esa variabilidad como un elemento de cuantificación del riesgo de un proyecto. 

La falta de certeza de las estimaciones del comportamiento futuro se puede asociar normalmente a una distribución de probabilidades de los flujos de caja generados por el proyecto. Su representación gráfica permite visualizar la dispersión de los flujos de caja, asignando un riesgo mayor a aquellos proyectos cuya dispersión sea mayor. 

Existen, sin embargo, formas precisas de medición que manifiestan su importancia principalmente en la comparación de proyectos o entre alternativas de un mismo proyecto. La más común es la desviación estándar, que se calcula mediante la expresión 

El riesgo en los proyectos - II

Una diferencia menos estricta entre riesgo e incertidumbre indentifica al riesgo como la dispersión de la distribución de probabilidades del elemento en estudio o los resultados calculados, mientras que la incertidumbre es el grado de falta de confianza respecto a que la distribución de probabilidades estimadas sea la correcta. John R. Cañada' señala y analiza ocho causas del riesgo e incertidumbre en los proyectos. 

Entre éstas cabe mencionar el número insuficiente de inversiones similares que puedan proporcionar información promediable; los prejuicios contenidos en los datos y su apreciación, que inducen efectos optimistas o pesimistas, dependiendo de la subjetividad del analista; los cambios en el medio económico externo que anulan la experiencia adquirida en el pasado, y la interpretación errónea de los datos o los errores en la aplicación de ellos. 

Se han hecho muchos intentos para enfrentar la falta de certeza en las predicciones. Las "mejoras limitadas", que David B. Hertz2 señalaba como "esfuerzos con éxito limitado que parecen no haber llegado a alcanzar la meta para hacer frente a la incertidumbre", se han superado por diversas técnicas y modelos cuya aplicación ha permitido una evaluación de proyectos, que, aun con las limitaciones propias de tener que trabajar sobre la base de predicciones futuras, logra incorporar la medición del factor riesgo.

El riesgo en los proyectos - I

El riesgo de un proyecto se define como la variabilidad de los flujos de caja reales respecto a los estimados. Mientras más grande sea esta variabilidad, mayor es el riesgo del proyecto. 

De esta forma, el riesgo se manifiesta en la variabilidad de los rendimientos del proyecto, puesto que se calculan sobre la proyección de los flujos de caja. 

 Hay dos conceptos importantes de diferenciar: riesgo e incertidumbre. El riesgo define una situación donde la información es de naturaleza aleatoria, en que se asocia una estrategia a un conjunto de resultados posibles, cada uno de los cuales tiene asignada una probabilidad. La incertidumbre caracteriza a una situa- ción donde los posibles resultados de una estrategia no son conocidos y, en con- secuencia, sus probabilidades de ocurrencia no son cuantificables. La incertidumbre, por lo tanto, puede ser una característica de información incompleta, de exceso de datos, o de información inexacta, sesgada o falsa. La incertidumbre de un proyecto crece en el tiempo. 

El desarrollo del medio condicionará la ocurrencia de los hechos estimados en su formulación. La sola mención de las variables principales incluidas en la preparación de los flujos de caja deja de manifiesto el origen de la incertidumbre: el precio y calidad de las materias primas; el nivel tecnológico de producción; las escalas de remuneraciones; la evolución de los mercados; la solvencia de los proveedores; las variaciones de la demanda, tanto en cantidad, calidad como en precio; las políticas del gobierno respecto al comercio exterior (sustitución de importaciones, liberalización del comercio exterior), la productividad real de la operación, etcétera.

Análisis de riesgo

En el capítulo anterior se estudiaron los criterios para definir la conveniencia de una inversión basada en condiciones de certeza. Tal suposición, sin embargo, se adoptó sólo para presentar el estudio de los procedimientos optativos de evaluación de un proyecto. 

El comportamiento único de los flujos de caja supuesto en el capítulo anterior es incierto, puesto que no es posible conocer con anticipación cuál de todos los hechos que pueden ocurrir y que tienen efecto en los flujos de caja ocurrirá efectivamente. Al no tener certeza sobre los flujos futuros de caja que ocasionará cada inversión, se está en una situación de incertidumbre. 

Cada proyecto tiene asociado cierto grado de riesgo que no puede excluirse de su evaluación, puesto que hará variar su nivel de aceptabilidad respectivo. El objetivo de este capítulo es analizar el problema de la medición del riesgo en los proyectos y los distintos criterios de inclusión y análisis para su evaluación. No se incluye en este estudio el riesgo de la cartera, que, aunque es un tema de alto interés, escapa al objetivo de este texto.